Подробные решения 27-х заданий из демонстрационных вариантов ЕГЭ по информатике за 2016, 2018-2023 г.
У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные
Дано два входных файла ( файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте ( все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
Типовой пример организации данных во входном файле
61 1002 2005 47 38 210 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1·2 + 3·1 + 5·1 + 6·1 + 8·2.
Решение:
Что просят?
Найти такой пункт куда дешевле доставлять контейнеры с пробирками из других пунктов. Для этого нужно посчитать стоимость доставки для каждого пункта.
Как считать стоимость?
Пусть у нас только 4 пункта:
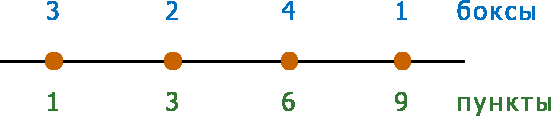
Посчитаем стоимость доставки по формуле |расстояние| * боксы (для каждого пункта считаем расстояние к нему, умноженное на кол-во боксов каждого пункта):
| |1-1|×3+ | |3-1|×3+ | |6-1|×3+ | |9-1|×3+ |
| |1-3|×2+ | |3-3|×2+ | |6-3|×2+ | |9-3|×2+ |
| |1-6|×4+ | |3-6|×4+ | |6-6|×4+ | |9-6|×4+ |
| |1-9|×1= | |3-9|×1= | |6-9|×1= | |9-9|×1= |
| 32 | 24 | 24 | 48 |
Последние числа – это стоимость доставки боксов в текущий пункт. Например, стоимость доставки в первый пункт равна 32, во второй 24 и т.д. Результаты получены квадратичным(неэффективным) алгоритмом:
cst[] = [0 0 0 0 0 0] ; массив стоимостей dst[] = [1 2 5 7 8 10]; расположения пунктов box[] = [2 3 1 1 1 2]; боксы (контейнеры) Для i от 1 до N; dst[i] - предполагаемый пункт ; dst[j] – отсюда повезём боксы(box[j]) в i-й пункт Для j от 1 до N cst[i] = cst[i] + |dst[i]-dst[j]| × box[j]
Эффективный алгоритм
Получим числа 32, 24, 24, 48 эффективным(не квадратичным) способом. Для начала вычислим первое число (32):
cst[] = [0 0 0 0] ; массив стоимостей Для i от 1 до N ; cst[1] = |dst[i]-dst[1]| × box[i]; cst[] = [38 0 0 0] получили первое число
32 – это стоимость доставки в 1-й пункт из всех остальных пунктов. Сюда входят стоимости всех боксов справа от первого пункта и не входят боксы собственно 1-го пункта(1-й пункт не доставляет боксы сам себе – |1-1|×3=0).
Чтобы вычислить стоимости доставок в следующие пункты, воспользуемся данными о доставках, хранящихся в предыдущих пунктах. Когда мы будем получать стоимости доставок в следующие пункты, вычислять заново все боксы не нужно. Нужно лишь на каждом шаге подкорректировать данные предыдущих пунктов. Например, рассмотрим вычисление стоимости для 2-го пункта:
У 2-го пункта, предыдущий пункт – 1, его стоимость 32. Это число, для 2-го пункта, содержит недостающие и лишние данные. Недостающие данные – это та стоимость, которую мы не учли для 1-го пункта: для 1-го пункта не учтены 3 бокса (свои боксы себе возить ненужно), поэтому их нужно добавить для 2-го пункта. Лишние данные – это та стоимость, которая вошла при перевозки боксов всех пунктов, но на расстояние между 2-м и 1-м пунктом. Значит нужно вычесть длину смещения между нынешним пунктом(2) и предыдущим(1) умноженное на все боксы (другими словами, после смещения вправо предыдущая стоимость содержит лишнее значение равное длине смещения умноженное на все боксы).
Вычитание лишних и добавление недостающих данных
Вычитание лишних данных для 2-го пункта:
32 – (3-1)*2 + (3-1)*4 + (3-1)*1
но лучше так:
32 – (3-1)*(2 + 4 + 1)
Такое упрощение позволит получить оптимальный способ решения задачи – вторая скобка содержит сумму всех боксов(без 1-го пункта), и поскольку кол-во боксов известно заранее, их сумму можно вычислить один раз, для одного пункта, чтобы затем использовать для остальных пунктов. Например, для 3-го пункта вычитание будет таким:
…– (6-3)*(4 + 1)
т.е. для 3-го пункта двойку убрали.
Теперь рассмотрим добавление недостающих данных для 2-го пункта:
…+ (3-1)*3
для 3-го:
…+ (6-3)*(3+2)
Общая картина вычислений начиная со 2-го пункта (1-й пункт вычислен заранее неэффективным способом):
32 – (3-1)*(2 + 4 + 1) + (3-1)*3 = 24 24 – (6-3)*(4 + 1) + (6-3)*(3 + 2) = 24 24 – (9-6)*(1) + (9-6)*(3 + 2 + 4) = 48
boxes = 10 ; все боксы – посчитанные на 1-м проходе left = box[1];left=3 боксы слева right = boxes - left; right=7 боксы справа Для i от 2 до N; начинаем со второго пункта cst[i] = cst[i-1] - (dst[i] - dst[i-1]) * right + (dst[i] - dst[i-1]) * left; dst[i]-dst[i-1] – расстояние на которое мы переместились слева направо ; cst[i] – стоимость доставки в текущий пункт ; cst[i-1] – ранее вычисленная стоимость доставки, которую нужно подкорректировать ; настроим боксы от которых ушли и к которым пришли right = right - box[i] left = left + box[i]; получение числа 24 из 32 для 2-го пункта: ; 24 = 32 – (3 - 1) * 7 + (3 - 1) * 3 Настраиваем указатели для 3-го пункта ; right = 7-2 к этим пришли, зн. их вычтем ; left = 3+2 от этих ушли, зн. их добавим ; получение числа 24 из 24 для 3-го пункта: ; 24 = 24 – (6 - 3) * 5 + (6 - 3) * 5 Настраиваем указатели для 4-го пункта ; right = 5-4 к этим пришли, зн. их вычтем ; left = 5+4 от этих ушли, зн. их добавим ; получение числа 48 из 24 для 4-го пункта: ; 48 = 24 – (9 - 6) * 1 + (9 - 6) * 9
Полный код на Python
f=open('27_B.txt')
n=int(f.readline())
dst=[0]*n #расположения пунктов
box=[0]*n #контейнеры(боксы)
cst=[0]*n #стоимости
boxes=0 #все контейнеры(боксы)
k=36
for i in range (n):
x,y=map(int,f.readline().split())
dst[i]=x
box[i]=y//k + 1*(y%k!=0)
cst[0] += (dst[i]-dst[0])*box[i]
boxes += box[i]#суммируем все боксы
left = box[0]
right = boxes - left
for i in range (1,n):
cst[i] = cst[i - 1] - (dst[i] - dst[i - 1]) * right \
+ (dst[i] - dst[i - 1]) * left
right -= box[i]
left += box[i]
print(min(cst))
Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них.
Входные данные
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число, не превышающее 10 000.
Пример организации исходных данных во входном файле:
7134938595
В ответе укажите два числа: сначала значение искомой длины для файла А, затем – для файла B.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго
Эффективный поиск подпоследовательности
Рассмотрим суть эффективного поиска числовой подпоследовательности, сумма которой делится на нужное число без остатка. Для простоты возьмём такую последовательность, у которой две подпоследовательности делятся, например, на 10: [2 1
Просуммируем каждое число последовательности и разместим полученные суммы под числами последовательности:
| 2 | 1 | 5 | 7 | 8 | 4 | 12 | 8 | Последовательность |
| 2 | 3 | 8 | 15 | 23 | 27 | 39 | 47 | Суммы |
Чтобы найти первую подпоследовательность (5 7 8), посмотрим на сумму, которая стоит под числом 8. Это число 23. Его можно превратить в 20, если вычесть 3, а число 3 стоит как вторая сумма. Значит, для поиска подпоследовательности, сумма которой делится на 10 без остатка, нужно из одной суммы вычесть другую: 2+1+5+7+8 – 2+1 = 5+7+8.
Подпоследовательность 2 1 называют «хвостом» подпоследовательности 2 1 5 7 8, который нужно вычесть, чтобы получить нужный результат:
| 2 | 1 | 5 | 7 | 8 | |
| 2 | 1 | Хвост | |||
| 5 | 7 | 8 | Нужный результат |
Как теперь найти, что из общей суммы: 2+1+5+7+8 нужно вычесть именно 2+1, чтобы гарантированно получить результат, который делится на 10 без остатка?
Есть такое правило:
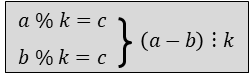
…которое говорит, что если два числа при делении на k дают один и тот же остаток, то их разность делится на k без остатка. У нас a – это сумма 2+1+5+7+8, b – это сумма 2+1, а k это 10
Теперь исследуем остатки, которые получатся при делении каждой суммы на 10:
| 2 | 1 | 5 | 7 | 8 | 4 | 12 | 8 | Последовательность |
| 2 | 3 | 8 | 15 | 23 | 27 | 39 | 47 | Суммы |
| 2 | 3 | 8 | 5 | 3 | 7 | 9 | 7 | Остатки |
Есть одинаковые остатки! Это поможет найти и вычесть хвост у последовательности, и задача решена. Рассмотрим как следить за остатками.
Массив остатков
Наша задача сохранить все суммы, и пометить какой у них остаток при делении на k. Для этого создадим массив tailSum размером k. Индекс элемента этого массива – это остаток при делении очередной суммы на k. Эту сумму нам нужно занести в массив по её остатку. Тем самым мы пометим под каким остатком хранится та или иная сумма.
Так вот, один и тот же остаток должен встретится ещё раз в процессе суммирования. А это значит, что в массиве tailSum – по индексу остатка – уже сохранена ранее сумма, и если её вычесть из общей суммы(totalSum), – получится нужная сумма(curSum).
Рассмотрим всё это по шагам:
m = [2 1 5 7 8 4 12 8] k = 10 totalSum = 0 tailSum - [0 0 0 0 0 0 0 0 0 0] 1 шаг totalSum = 2;если tailSum[2 % k] = 0 ;то в tailSum[2 % k] = 2 tailSum - [0 0 2 0 0 0 0 0 0 0] 2 шаг totalSum = 3;если tailSum[3 % k] = 0 ;то в tailSum[3 % k] = 3 tailSum - [0 0 2 3 0 0 0 0 0 0] 3 шаг totalSum = 8;если tailSum[8 % k] = 0 ;то в tailSum[8 % k] = 8 tailSum - [0 0 2 3 0 0 0 0 8 0] 4 шаг totalSum = 15;если tailSum[15 % k] = 0 ;то в tailSum[15 % k] = 15 tailSum - [0 0 2 3 0 15 0 0 8 0] 5 шаг totalSum = 23;если tailSum[23 % k] != 0 ;то curSum = totalSum - tailSum[23 % k] 23 – 3 curSum = 20;нужная сумма
Программа на Python
m = [2,1,5,7,8,4,12,8]#данная последовательность n = len(m) k = 10 totalSum = 0 tailSum = [0]*k#[0 0 0 0 0 0 0 0 0 0] for i inrange (n): totalSum += m[i] r = totalSum % k if tailSum[r] == 0:#был ли такой остаток или нет? # такого остатка ещё не было => сохраняем сумму(потенциальный хвост) и помечаем под каким она остатком tailSum[r] = totalSum else:#такой остаток уже есть => вычитаем предыдущую сумму(хвост) из текущей curSum = totalSum - tailSum[r]
Длина подпоследовательности
Длина подпоследовательности – это разность между двумя значениями циклической переменной i. Первое значение (начало подпоследовательности) сохраним в массив tailLen. Второе значение (конец подпоследовательности). Первое значение соответствует моменту, когда мы сохраняли первую сумму для отсечения хвоста, второе – когда нашли в tailSum не нулевое значение. Следовательно, tailLen аналогичен tailSum:
… tailLen = [0]*k for i inrange (n): … if tailSum[r] == None: …#i – первое значение длины - сохраним в tailLen tailLen[r] = i else: …#i – второе значение длины - из него вычтем первое curLen = i - tailLen[r]
Максимальная и самая короткая сумма
Максимальная сумма находится обычным делом. Кроме этого, текущая сумма может быть равной максимальной(встретились две одинаковые нужные суммы), тогда нужно убедиться, что кол-во элементов текущей суммы(currLen) меньше кол-ва элементов максимальной суммы(maxSum). Раз так – модифицируем переменные maxSum и minLen текущими значениями суммы и длины:
… maxSum = minLen = 0 for i inrange (n): … else: … if curSum > maxSum or \ (curSum == maxSum and curLen < minLen): maxSum = curSum minLen = curLen
Полный код на Python (подпоследовательность не сначала)
m = [2,1,5,7,8,4,12,8] n = len(m) tailSum=[0]*k tailLen=[0]*k minLen=float('inf' ) totalSum=curSum=maxSum=curLen=0 for i inrange (n): totalSum += m[i] r = totalSum % k if tailSum[r] == 0: tailSum[r] = totalSum tailLen[r] = i else: curSum = totalSum - tailSum[r] curLen = i - tailLen[r] if curSum > maxSum or \ curSum == maxSum and curLen < minLen: maxSum = curSum minLen = curLen print(minLen,)
Если нужная подпоследовательность вначале массива, то остаток r равен нулю, а totalSum – есть найденная сумма. При увеличении totalSum – сумма будет увеличиваться, значит проверять на максимум не нужно. Остаётся проверить длину на минимум:
Полный код на Python (подпоследовательность сначала)
m=[5,7,8,8,4,12] n = len(m) tailSum=[0]*k tailLen=[0]*k minLen=float('inf' ) totalSum=curSum=maxSum=curLen=0 for i inrange (n): totalSum += m[i] r = totalSum % k if r == 0 and i < minLen: maxSum = totalSum minLen = i+1 print(minLen,)
Полный код на Python
f=open('27_B.txt')
n=int(f.readline())
k=43
totalSum=curSum=maxSum=curLen=0
tailSum=[0]*k
tailLen=[0]*k
minLen=float('inf' )
for i in range (n):
totalSum+=int(f.readline())
r=totalSum%k
if r!=0:
if tailSum[r] == 0:
tailSum[r] = totalSum
tailLen[r] = i
else:
curSum = totalSum - tailSum[r]
curLen = i - tailLen[r]
if curSum > maxSum or \
curSum == maxSum and curLen < minLen:
maxSum = curSum
minLen = curLen
elif i < minLen:
maxSum = totalSum
minLen = i+1
print(minLen)
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно.
Программа должна напечатать одно число – максимально возможную сумму, соответствующую условиям задачи.
Входные данные
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000.
Пример организации исходных данных во входном файле:
61 35 126 95 43 31 1
Для указанных входных данных значением искомой суммы должно быть число 32.
В ответе укажите два числа: сначала значение искомой длины для файла А, затем – для файла B.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго
Сумма максимумов
Выберем данную последовательность из шести пар и просуммируем максимальное число каждой пары:
| 1 | 3 |
| 5 | 12 |
| 6 | 9 |
| 5 | 4 |
| 3 | 3 |
| 1 | 1 |
l = [1,5,6,5,3,1]# первое число пары r = [3,12,9,4,3,1]# второе число пары n = len(l)# а можно и len(r) s = 0 for i inrange (n): a=l[i]; b=r[i] s += max(a, b)
Сумма будет 33(переменная s). Если бы сумма не делилась на 3, то она бы являлась ответом. Но она делится, значит, одно максимальное число(неважно какое), которое попало в сумму, нужно поменять на минимальное из той же пары – да так поменять, что это минимальное в паре число, должно быть самым минимальным среди всех минимальных(это условие максимально возможной суммы).
Поиск нужного минимума
В нашем примере, вместо максимального числа 5, нужно использовать 4. Как его найти эффективно?
В процессе суммирования находим минимальную разницу между парами, которая не делится на 3:
... min = 10001 for i inrange (n): ... d = abs(a-b) if(d%3 != 0) and (d < min): min = d
Единица в последней паре не подойдёт в качестве минимума, потому что оба числа пары равны и от того первое выражение условия даст отрицание.
Вывод на экран
Переменную min применим, если сумма делится на 3, иначе выведем сумму:
... for i inrange (n): ... if s%3==0: print(s-min) else: print(s)
Полный код на Python
f = open('27.txt')
n = int(f.readline())
s = 0
min = 10001
for i in range (n):
a,b = map(int,f.readline().split())
s += max(a,b)
d = abs(a-b)
if(d%3 != 0) and (d < min):
min = d
# вывод на экран
if s%3==0:
print(s-min)
else:
print(s)
На вход программы поступает последовательность из n целых положительных чисел. Рассматриваются все пары элементов последовательности ai и aj, такие что i < j и ai > aj (первый элемент пары больше второго; i и j – порядковые номера чисел в последовательности входных данных). Среди пар, удовлетворяющих этому условию, необходимо найти и напечатать пару с максимальной суммой элементов, которая делится на m = 120. Если среди найденных пар максимальную сумму имеют несколько, то можно напечатать любую из них.
Описание входных и выходных данных
В первой строке входных данных задаётся количество чисел n (2 ≤ n ≤ 12 000). В каждой из последующих n строк записано одно целое положительное число, не превышающее 10 000.
В качестве результата программа должна напечатать элементы искомой пары. Если таких пар несколько, можно вывести любую из них. Гарантируется, что хотя бы одна такая пара в последовательности есть.
Пример входных данных:
6601406110030059
Пример выходных данных для приведённого выше примера входных данных:
140 100
Пояснение.Из шести заданных чисел можно составить три пары, сумма элементов которых делится на m=120: 60+300, 140+100 и 61+59. Во второй и третьей из этих пар первый элемент больше второго, но во второй паре сумма больше.
Требуется написать эффективную по времени и памяти программу для решения описанной задачи.
Поиск пары
Пары будут двух типов: каждый элемент пары не кратный m, а сумма элементов кратна, и каждый элемент пары кратный m – сумма также кратна.
Рассмотрим, как искать пару, сумма которой кратна m, но каждый элемент не кратный. Есть правило:
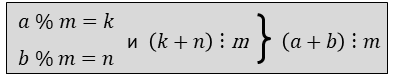
которое говорит, что если два числа при делении на m дают остатки, сумма которых делится на m, то и сумма чисел делится на m. Например: пусть m=5, a=8 и b=12, тогда:
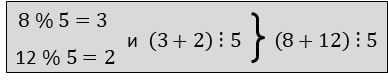
Теперь как найти, среди последовательности чисел, пару 8 и 12, сумма которой делится на 5.
Удобнее всего через так называемый массив остатков r размером m. На самом деле элементы этого массива – это числа последовательности, а индексы этих элементов – остатки от деления элементов на m. Пусть наши 8 и 12 расположены в такой последовательности: [ 8 14 12 ], тогда массив остатков r[m] будет таким:
| 0 | 0 | 0 | 0 | 0 | массив r |
| 0 | 0 | 0 | 0 | 14 | r[14 % 5]=14 |
| 0 | 0 | 0 | 8 | 14 | r[8 % 5]=8 |
| 0 | 0 | 12 | 8 | 14 | r[12 % 5]=12 |
| [0] | [1] | [2] | [3] | [4] | индексы-остатки |
Мы ищем пару по индексам: пусть под одним индексом есть ненулевой элемент массива, тогда если мы обнаруживаем, что есть ещё ненулевой элемент, индекс которого даёт сумму с первым индексом кратную 5, то сумма элементов также кратна 5.
Как найти 2-й индекс? По m и по 1-му индексу: 2-й индекс = m – 1-й индекс. В нашем случае 2-й индекс это 3, а 1-й – это 2. Всё потому что, когда мы проверяем число 8(индекс 3) - его пара под индексом 2 хранит нулевое значение и поэтому по 3-му индексу пару найти невозможно:
| 0 | 0 | 0 | 8 | 14 | r[5 - 3] это 0 |
| [0] | [1] | [2] | [3] | [4] | индексы-остатки |
Но когда проверяем число 12 (индекс 2) - его пара под индексом 3 хранит не нулевое значение:
| 0 | 0 | 0 | 8 | 14 | |
| 0 | 0 | 12 | 8 | 14 | r[5 - 2] это 12 |
| [0] | [1] | [2] | [3] | [4] | индексы-остатки |
Вот тогда то, мы и находим нужную пару:
m = 5 d = [8,14,12]# последовательность r = [0,0,0,0,0]# массив «остатков» for i inrange (len (d)): a = d[i]# a удобнее чем d[i] p = a % m if r[m-p]>0:# false при a=8, true при a=12 print (r[m-p], " ", a)# 8 12 r[p] = a# заполняем массив остатков (пока они различны)
Первый больше второго
По условию, первый элемент пары должен быть больше, значит наша последовательность - [ 8 14 12 ] - не содержит нужной пары. Поменяем местами 8 и 12 и в условии учтём, что предыдущий сохранённый элемент массива остатков больше чем текущий:
m = 5 d = [12,14,8]# последовательность r = [0,0,0,0,0]# массив «остатков» for i inrange (len (d)): a = d[i]# a удобнее чем d[i] p = a % m if r[m-p]>a:# предыдущий r[m-p] больше текущего a print (r[m-p], " ", a)# 8 12 r[p] = a# заполняем массив остатков (пока они различны)
Теперь предыдущая последовательность - в связи с тем, что она неправильная - не будет найдена.
Пара с максимальной суммой
По условию, нужная пара должна давать максимальную сумму среди всех нужных пар, т.е. пар может быть несколько, а выбрать нужно ту, которая даёт максимальную сумму. Добавим в условие выражение, которое сравнивает сумму текущей пары с парой сохранённой ранее
Кроме этого, нужно учесть, что в последовательности может быть не одно число с одним и те же остатком, тогда если оно больше предыдущего, то в массиве остатков меняем предыдущее на текущее. Если остатки разные, то массив остатков будет заполняться, так же как и раньше:
m = 5 d = [22,38,8,14,2]# Нужная 38 и 2 среди ещё одной 22 и 8 r = [0,0,0,0,0]# массив «остатков» left = 0; right = 0# элементы нужной пары for i inrange (len (d)): a = d[i]# a удобнее чем d[i] p = a % m if r[m-p]>a and r[m-p]+a > left+right: left = r[m-p] right = a if a>r[p]:# a > предыдущего с таким же остатком r[p] = a# значит заменим его на a print (l, " ", r)# 38 2
Один тип пары мы выбрали, переходим к другому типу – каждый элемент которого кратный m.
Пара элементов кратные m
Случай с одной парой, причём пусть, первый элемент меньше второго(далее исправим): [10, 14, 15]
m = 5 d = [5,14,10]# последовательность r = [0,0,0,0,0]# массив «остатков» for i inrange (len (d)): a = d[i]# a удобнее чем d[i] p = a % m if r[m-p]>0:# false при a=8, true при a=12 print (r[m-p], " ", a)# 8 12 r[p] = a# заполняем массив остатков (пока они различны)
Первый больше второго(среди кратных m)
Поменяем местами 5 и 10, затем изменим условие:
m = 5 d = [10,14,5]# последовательность r = [0,0,0,0,0]# массив «остатков» for i inrange (len (d)): a = d[i]# a удобнее чем d[i] p = a % m if r[0]>a:# предыдущий r[0] больше текущего a print (r[0], " ", a)# 10 5 r[p] = a# заполняем массив остатков (пока они различны)
Теперь предыдущая последовательность, в связи с тем, что она неправильная, не будет найдена.
Пара с максимальной суммой(среди кратных m)
Аналогично соответствующему пункту данной задачи добавим переменные для максимальных элементов пар и изменим условие:
m = 5 d = [10,35,5,14,15]# Нужная 35 и 15, ненужная 22 и 8 r = [0,0,0,0,0]# массив «остатков» left = 0; right = 0# элементы нужной пары for i inrange (len (d)): a = d[i]# a удобнее чем d[i] p = a % m if r[0]>a and r[0]+a > left + right: left = r[0] right = a if a>r[p]:# a > предыдущего с таким же остатком r[p] = a# значит заменим его на a print (l, " ", r)# 35 15
Теперь учтём, что может быть два типа пар.
Полный код на Python
d = [10,35,5,14,15,22,38,8,14,2] m = 120 r = [0] * m# числа, которых ищут по остатку left=0; right=0 n =len (d) for i inrange (n): a = d[i] p = a % m if p == 0:# кратные m if r[0] > a and r[0] + a > left+right: left = r[0] right = a else:# не кратные m if r[m-p]>a and r[m-p]+a > left+right: left = r[m-p] right = a if a>r[p]:# a > предыдущего с таким же остатком r[p] = a print(l," ",r)
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности, находящихся на расстоянии не меньше чем 4 (разница в индексах элементов пары должна быть 4 или более, порядок элементов в паре неважен). Необходимо определить количество таких пар, для которых произведение элементов делится на 29.
Описание входных и выходных данных
В первой строке входных данных задаётся количество чисел N (4 ≤ N ≤ 1000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 10 000.
В качестве результата программа должна вывести одно число: количество пар элементов, находящихся в последовательности на расстоянии не меньше чем 4, в которых произведение элементов кратно 29.
Пример входных данных:
7582354129
Пример выходных данных для приведённого выше примера входных данных:
5
Пояснение.Из 7 заданных элементов с учётом допустимых расстояний между ними можно составить 6 произведений: 58·4, 58·1, 58·29, 2·1, 2·29, 3·29. Из них на 29 делятся 5 произведений.
Требуется написать эффективную по времени и памяти программу для решения описанной задачи.
Программа считается эффективной по времени, если при увеличении количества исходных чисел N в k раз время работы программы увеличивается не более чем в k раз.
Внимание! Для простоты, вместо деления на 29 будем проверять на чётность.
Эффективный алгоритм по времени, но не по памяти
Будем умножать конкретное число x с остальными числами последовательности, которые стоят на расстоянии ≥ 4 от x. Следовательно, ближайшие к x три числа пропускаем мимо. x.
Закрасим ненужные 3 числа красным, x – зелёным, а умножаемые с x–ом числа – синим цветом.
Может быть два случая:
- x – чётный
- x – нечётный
Тогда суммируем либо все синие числа(случай 1), либо только те синие, которые делятся на 2 (случай 2).
В 1-м случае кол-во чётных результатов будет равно кол-ву произведений x–а с числами синего цвета:
шаг 1
| 8 | 3 | 4 | 7 | 6 | 2 | 1 | 4 |
одно произведение: 6 * 8, здесь x = 6, он на 5-ом месте последовательности (нумерация с 1)
шаг 2
| 8 | 3 | 4 | 7 | 6 | 2 | 1 | 4 |
два произведения: 2 * 8 и 2 * 3, здесь x = 2, он на 2-ом месте последовательности
шаг 4
| 8 | 3 | 4 | 7 | 6 | 2 | 1 | 4 |
четыре произведения: 4 * 8, 4 * 3, 4 * 4, 4 * 7, здесь x = 4, он на 8-ом месте последовательности
В 2-м случае кол-во чётных результатов будет равно только кол-ву чётных синих чисел:
шаг 3
| 8 | 3 | 4 | 7 | 6 | 2 | 1 | 4 |
два произведения: 1*8 и 1*4, здесь x = 1, он на 7-ом месте последовательности
Для 1-го случая считать чётные произведения будет разница положения x–а и кол-во розовых чисел:
count = count + x – 3
Для 2-го случая понадобится переменная, которая считает чётные синие числа
count = count + b;где b уже знает сколько чётных синих
Остаётся считать кол-во чётных синих чисел:
b = b + 1
Полный код на Python
d = 4#расстояние до ближайшего нужного числа a = [8,3,4,7,6,2,1,4] n = len(a) count = 0#кол-во чётных пар всего b = 0#кол-во чётных синих чисел for i in range(d,n):#прицеливаемся на x=6 if a[i-d]%2 == 0: b += 1 if a[i]%2 == 0:#x делится на то что нужно? count += i-d+1#count=count+x-3 else: count += b print(count)
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре не важен). Необходимо определить количество пар, для которых произведение элементов делится на 26.
Описание входных и выходных данных
В первой строке входных данных задаётся количество чисел N (4 ≤ N ≤ 1000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 10 000. В качестве результата программа должна напечатать одно число: количество пар, в которых произведение элементов кратно 26.
Пример входных данных:
4261339
Пример выходных данных для приведённого выше примера входных данных:
4
Пояснение.Из четырёх заданных чисел можно составить 6 попарных произведений: 2·6, 2·13, 2·39, 6·13, 6·39, 13·39 (результаты: 12, 26, 78, 78, 234, 507). Из них на 26 делятся 4 произведения (2·13=26; 2·39=78; 6·13=78; 6·39=234).
Требуется написать эффективную по времени и по памяти программу для решения описанной задачи.
Программа считается эффективной по времени, если при увеличении количества исходных чисел N в k раз время работы программы увеличивается не более чем в k раз.
Решение
Пример входных данных неудачный: он не содержит чисел 26, поэтому мы не можем учесть такие пары, в которых либо ОБА элемента делятся на 26, либо ТОЛЬКО ОДИН. Пусть будет такая последовательность: 26 3 8 52 78. Из неё получаем неповторяющиеся пары: 26-3, 26-8, 26-52, 26-78, 3-8, 3-52, 3-78, 8-52, 8-78, 52-78. Теперь посчитаем, сколько будет произведений пар, которые делятся на 26.
ОБА элемента делятся на 26
Если оба элемента делятся на 26, то и их произведения тоже делятся. Из неповторяющихся пар, есть три пары, у которых оба элемента делятся на 26: 26-52, 26-78, 52-78. Формула, которая вычисляет кол-ва таких пар: (n26·(n26-1))/2, где n26 – это количество чисел в последовательности, которые делятся на 26. У нас n26=3(26,52 и 78), значит (3·(3-1))/2=3
ТОЛЬКО ОДИН элемент делится на 26
Шесть пар, у которых только один элемент делится на 26: 26-3, 26-8, 3-52, 3-78, 8-52, 8-78. Формула, которая вычисляет кол-ва таких пар: n26·(n-n26), где n – это количество чисел в последовательности. У нас n=5, значит 3·(5-3)=6
26=2·13
Теперь, случай, где элементы не кратны 26, но их произведение дадут число 26. Это число можно получить по двум множителям: 2 и 13. Значит нужно посчитать кол-во пар, у которых один элемент 2, другой 13. Для этого есть формула: n2·n13, где n2 – это кол-во чисел, которые делятся на 2 и n13 – кол-во чисел, которые делятся на 13.
Полный код на Python
f = open('2018_27.txt') #4 2 6 13 39
n = int(f.readline())#n=4
n26 = n2 = n13 = 0
for i in range (n):
x = int(f.readline())
if x%26 == 0:
n26 += 1
elif x%13 == 0:
n13 += 1
elif x%2 == 0:
n2 += 1
print((n26*(n26-1))//2+n26*(n-n26)+n2*n13)
В физической лаборатории проводится долговременный эксперимент по изучению гравитационного поля Земли. По каналу связи каждую минуту в лабораторию передаётся положительное целое число – текущее показание прибора «Сигма 2015». Количество передаваемых чисел в серии известно и не превышает 10 000. Все числа не превышают 1000. Временем, в течение которого происходит передача, можно пренебречь. Необходимо вычислить « бета-значение» серии показаний прибора – минимальное чётное произведение двух показаний, между моментами передачи которых прошло не менее 6 минут. Если получить такое произведение не удаётся, ответ считается равным –1.
Напишите программу для решения поставленной задачи, которая будет эффективна как по времени, так и по памяти (или хотя бы по одной из этих характеристик). Программа считается эффективной по времени, если время работы программы пропорционально количеству полученных показаний прибора N, т.е. при увеличении N в k раз время работы программы должно увеличиваться не более чем в k раз. Программа считается эффективной по памяти, если размер памяти, использованной в программе для хранения данных, не зависит от числа N и не превышает 1 килобайта.
Входные данные представлены следующим образом. В первой строке задаётся число N – общее количество показаний прибора. Гарантируется, что N > 6. В каждой из следующих N строк задаётся одно положительное целое число – очередное показание прибора.
Пример входных данных:
1112455317232120191817
Программа должна вывести одно число – описанное в условии произведение либо –1, если получить такое произведение не удаётся.
Пример выходных данных для приведённого выше примера входных данных: 54
Решение
Пусть для простоты расстояние будет не 6, а 3, и возьмём небольшие числа: 6 1 3 5 7 9 2 4 8. После того как составим алгоритм заменим 3 на 6.
Множители на расстоянии
Сохраним 1-ые 3 элемента входных данных в массив. Затем настроимся к оставшимся числам последовательности:
a = [6 1 3 5 7 9 2 4 8] m = [6 1 3]# сохраняем первые 3 for i inrange (3,n):# i = [3..n)
Получилась заготовка для обращений чисел, расположенных на расстоянии трёх элементов. Элементы массива m выделены синим цветом, а нужные элементы массива a – зелёным.
| 6 | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 8 |
Умножение
Схема умножения для первых трёх шагов:
| 6 | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 8 |
| 6 | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 8 |
| 6 | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 8 |
Перед умножением элемента массива m, проверим его на минимум и сохраним его в minx:
… minx = 1001 for i inrange (3,n):# a[3] = 5 if m[i%3] < minx:#[3%3]=0, [4%3]=1, [5%3]=2 minx = m[i%3]
На третьем шаге в minx будет 1 – это значит, что не нужно беспокоиться о «пропущенном» произведении: 6*7, 6*9… – раз нужно минимальное произведение, то проверять произведения 6-ки со всеми кроме ближайших по условию не нужно.
Теперь умножаем числа расположенные на расстоянии 3-х элементов:
… x = a[i] # a[i] = 5 p = minx * x
Проверим произведение на минимум и чётность:
…
if (p%2==0 and p < minp):
minp = p
minp – хранит минимальное чётное произведение, которое будет результатом
Следующее умножение
Теперь самое интересное. В конце цикла заменяем текущий элемент массива m, на x, т.о., за три шага создаём следующую тройку для произведения:
…
m[i%3] = x # при i=3, m[0] = 5
| 5 | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 8 |
Т.е. когда, на втором шаге, будут умножаться 1 на 7 – в первом элементе массива m вместо 6 будет значение 5, которое через два шага будет умножаться на 2, и т.д. Так, выделены красным элементы массива m после трёх шагов цикла:
| 5 | 7 | 9 | 5 | 7 | 9 | 2 | 4 | 8 |
Теперь полный код, в котором заменено значение 3 на 6
Полный код на Python
a=[12,45,5,3,17,23,21,20,19,18,17] n=len(a)# n=11 m=[0]*6 minp=1000001;minx=1001 for i inrange (6): m[i]=a[i] for i inrange (6,n): if m[i%6] < minx: minx=m[i%6] x=a[i] p=minx*x if(p%2==0 and p < minp): minp=p m[i%6]=x# если ни одного произведения не нашлось, то выведем -1 if minp == 1000001: print (-1) else: print(minp)
0 Responses to “ЕГЭ 27 Демо”