Вспомним, что механическое движение – это изменение положения тела относительно других тел с течением времени.
Если мы свяжем с любым телом свою систему координат, то любое тело можно считать за ТО, значит одно и то же тело может занимать различное положение относительно других тел. Например, положение ручки на столе различное относительно стола и двери.
Но относительно не только положение, но и движение. Например, пассажир в стоящем поезде полагает, что он движется если будет смотреть в окно на движущийся поезд. А на самом деле он движется относительно поезда, но не относительно земли.
Поскольку, скорость – это характеристика движения, то и она также относительна. А что нам даёт относительное движение и относительная скорость?
Пусть есть неподвижная СО, например земля, пусть есть другая подвижная СО, которая движется относительно неподвижной и нам известно её движение (мы знаем её скорость и направление). Мы можем, находясь в неподвижной СО, определить движение тела относительно движущейся СО.
Или наоборот: мы знаем движение подвижной СО, знаем движение тела относительно подвижной СО, тогда мы можем найти движение тела относительно неподвижной СО, т.е. относительно земли.
Рассмотрим движение тела относительно двух разных СО, движущихся относительно друг друга: одна СО неподвижна, другая движется равномерно и прямолинейно.
Река, два берега, известно течение реки, плот плывёт вдоль течения, к плоту причалена лодка. На берегу и на плоту есть наблюдатели, оба наблюдают за лодкой. Лодка отчаливает от плота и движется к противоположному берегу равномерно и прямолинейно:

На интерактиве даны плот, который привязан к пирсу(зелёный прямоугольник), а к плоту причалена лодка. После нажатия на Move плот отвязывается от пирса, а лодка отчаливает от плота. Движение на интерактиве можно рассмотреть относительно трёх различных СО.
Нарисуем векторы перемещений лодки в двух СО: относительно берега и относительно плота:
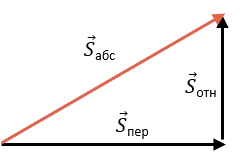
- Поскольку берег неподвижный, то первый вектор назовём абсолютным перемещением: Sабс.
- Поскольку плот движется, то второй вектор назовём относительным перемещением: Sотн.
- Река перенесла плот, а вместе с ней и лодку. Получим переносный вектор: Sпер.
Получили знакомую, по векторной сумме, тройку векторов:
Sабс = Sотн + Sпер
Поскольку в механике очень важно описывать движение, то нужно знать векторы скорости. Их легко получить, потому что эти перемещения совершены за одинаковый промежуток времени t, тогда разделим каждое перемещение на эти промежутки, получим три вектора скорости:
Sабс/t = Sотн/t + Sпер/t
или:
uабс = uотн + uпер
Это закон сложения скоростей. Он звучит так:
Скорость тела относительно неподвижной СО равна векторной сумме скорости тела относительно движущейся СО и скорости движущейся СО относительно неподвижной.
Закон сложения скоростей написан в векторной форме, это значит, что его можно использовать для самых разных случаев. Рассмотрим два простых, которые мы часто видим в жизни.
Скорый поезд обгоняет электропоезд. Мы едем в электропоезде. Скорость электропоезда 60 км/ч, а – скорого 90 км/ч. Найдите скорость скорого поезда относительно электропоезда.

Дано: uэ = 60 км/ч, uс = 90 км/ч. Найти: uотн
!!! Нужно уметь определять как связаны скорости uэ и uс к величинам закона сложения скоростей !!!
Поведём аналогию движения лодки и плота с движениями поездов: мы едем в электропоезде, а относительно нас едет скорый, тогда электропоезд сравниваем с плотом, а скорый поезд с лодкой.
Движение электропоезда обозначим как вектор переносной скорости: uэ = uпер (это скорость той СО, в которой находимся мы). А движение скорого – как вектор абсолютной скорости: uс = uабс (её увидел бы наблюдатель на дороге).
uотн – это скорость, которую видит пассажир электропоезда, когда смотрит на скорый. Или скорость, которую видит пассажир скорого поезда, когда смотрит на электропоезд.
uпер=uэ – это скорость, которую видит наблюдатель на земле, когда смотрит на электропоезд. Или скорость, которую видит пассажир электропоезда, когда смотрит на стоящего наблюдателя.
uабс=uс – это скорость, которую видит наблюдатель на земле, когда смотрит на скорый поезд. Или скорость, которую видит пассажир скорого поезда, когда смотрит на стоящего наблюдателя.
Подставим в закон сложения скоростей наши векторы:
uс = uотн + uэ
Мы ищем скорость скорого поезда относительно электропоезда – это uотн
Тогда: uотн = uс – uэ
Т.к. это векторы, то полученная формула справедлива как для попутного, так и для встречного движения. Докажем это:
Рассмотрим два случая: попутное и встречное движение.
а) Попутное движение. Уберём векторы, для этого нарисуем ось и спроецируем векторы:

uотн x = uс x – uэ x
Т.к. направления скоростей совпадают с направлением ОХ, то их проекции равны модулям скорости:
uотн x = uс – uэ = 90 км/ч – 60 км/ч = 30 км/ч
Итак, пассажир электропоезда видит две вещи: 1 скорость скорого поезда 30 км/ч, 2 эта скорость вдоль оси x.
Последняя формула ничего не говорит о том, где находится скорый – за или перед электропоездом, потому что она говорит только об относительной скорости, которая везде одинакова!
Формула с проекциями не зависит от того куда едет электропоезд и/или скорый поезд, потому что она совпадает с векторной формулой. Значит её можно учесть в случае б)
б) Встречное движение. Электропоезд движется туда же, а скорый – навстречу ему. Скорости те же. Спроецируем их на ось х:

uотн x = uс x – uэ x
uотн x = –uс – uэ = 90 км/ч – 60 км/ч = 30 км/ч
Минус говорит о движении против оси x.
Мы доказали, что векторная формула годиться для двух случаев, т.е. она не зависит от направления.
За 4 ч моторная лодка проходит против течения расстояние 48 км. За какое время она пройдёт обратный путь, если скорость течения равна 3 км/ч?
tпр, ℓ, uт
tпо-?
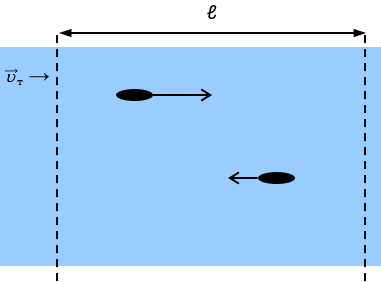
uабс = uотн + uпер
uотн – скорость лодки относительно воды, uпер – скорость реки.
На рисунке длины векторов скорости получаются путём сложения вектора скорости реки и векторов скоростей лодок относительно воды.
Если направление течения совпадает с направлением лодки, то обе скорости складываются, и полученная сумма связывается с ℓ и tпо:
uл + uт = ℓ / tпо (1)
Если лодка движется против течения, то uотн и uпер направлены противоположно . Например, если лодка проходит на 10 м влево относительно воды, но вода течёт вправо на 2 м, получается, что лодка прошла 10-2 м, т.е. скорости вычитаются, и полученная разность связывается с ℓ и tпр:
uл — uт = ℓ / tпр (2)
Законов сложения расстояний или времён нет, но есть закон сложения скоростей, поэтому можно связать скорости с теми величинами, которые есть. Вычтем одно равенство из другого – (1) — (2):
(uл + uт) — (uл — uт) = ℓ / tпо — ℓ / tпр
uл + uт — uл + uт = ℓ / tпо — ℓ / tпр
2uт = ℓ / tпо — ℓ / tпр
мы связали друг с другом все величины, которые у нас есть
2uт + ℓ / tпр = ℓ / tпо
(2uт·tпр + ℓ) / tпр = ℓ / tпо
tпо = tпр·ℓ/(2uт·tпр + ℓ)
по формуле видно, что дробь безразмерная величина
Моторная лодка за 1,5 ч доставляет почту из города в посёлок, расположенный ниже по течению реки. Сколько времени займёт обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения реки?
tпо, n,
uл=nuт

uабс = uотн + uпер
Добавим на рисунок ℓ и uт, их нет в условии, но в природе они есть, и они связаны с законом сложения скоростей.
Рассмотрим две абсолютные скорости, которые видны с берега – по течению и против. По течению – это сумма скорости лодки относительно воды (uотн) и скорости течения (uпер она же uт)
Свяжем эти абсолютные скорости с теми величинами, которые есть в задаче – tпо:
По течению: uл + uт = ℓ/tпо
Против течения: uл — uт = ℓ/tпр
Свяжем скорости лодки и течения:
nuт + uт = ℓ/tпо
nuт — uт = ℓ/tпр
вынесем за скобки uт:
uт(n+1) = ℓ/tпо(1)
uт(n-1) = ℓ/tпр(2)
(1)/(2):
[uт(n+1)/uт(n-1)] = (ℓ/tпо)·(tпр/ℓ)
tпр = tпо · (n+1)/(n-1) = 1,5ч·5/3 = 0,5·5 = 2,5ч
Для дроби из предыдущей задачи:
tпр = tпо·(n+1)/(n-1)
изучите случаи когда:
а) лодка быстрая,
б) лодка медленная,
в) скорость лодки равна скорости течения.
Решение:
а) Лодка быстрая – это значит, что скорость лодки во много раз больше(>>) скорости течения:
uл >> uт, значит n >> 1
Говорят, что n такая огромная, что её единица особо не увеличивает и особо не уменьшает. Следовательно, единицей можно пренебречь, поэтому дробь стремится к единице, тогда:
tпр ≈ tпо
Такая лодка будет плыть одинаковое расстояние против и по течению за почти одинаковое время.
б) Лодка медленная – это значит, что скорость лодки едва больше скорости течения, а n едва больше 1:
n ≈ 1, n > 1
перепишем дробь для n:
tпр = tпо·2 / малое число
Поскольку в знаменателе малое число, то tпр – большое число, значит:
tпр >> tпо
в) если скорости лодки и течения равны, это значит, что n = 1 и знаменатель равен нулю. В таких случаях дробь равна бесконечности, тогда время возврата tпр увеличивается до бесконечности, и лодка будет стоять на месте, потому что течение будет её возвращать на столько, на сколько она проплыла.
Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?
tэ, tчэ,
tч-?
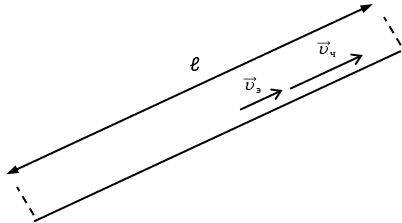
uабс = uотн + uпер
Добавим на рисунок величину ℓ, её нет в задаче, но в природе она есть, и она связана с законом сложения скоростей.
uэ = ℓ / tэ (скорость эскалатора или скорость стоящего человека, её видит наблюдатель за пультом эскалатора, когда смотрит на ступеньки или на неподвижного человека, ещё это uпер)
uч = ℓ / tч (скорость человека по неподвижному эскалатору или скорость, которую видит стоящий на эскалаторе человек, когда смотрит на бегущего по эскалатору, ещё это uотн)
uл + uэ = ℓ / tчэ (скорость, которую видит наблюдатель за пультом эскалатора, когда смотрит на бегущего по эскалатору, ещё это uабс)
(Для простоты, величины в скобках: uабс, uотн и uпер указаны без векторов, на самом деле, каждая величина может быть знаковой и беззнаковой, всё зависит от того где бежит человек: относительно стоящего за ним, или перед ним, поэтому в строгом смысле, величины эти – векторы)
В третье уравнение подставим правые части первого и второго
ℓ / tч + ℓ / tэ = ℓ / tчэ
· 1 / ℓ
1 / tч + 1 / tэ = 1 / tчэ
1 / tч = 1 / tчэ — 1 / tэ
1 / tч = (tэ — tчэ) / tэ·tчэ
tч = tчэ·tэ / (tэ — tчэ)
Эскалатор метро спускает идущего по нему вниз человека за 1 мин. Если человек будет идти вдвое быстрее, то он спустится за 45 с. Сколько времени спускается человек, стоящий на эскалаторе?
t1, t2, n,
u2=nu1
t0-?

uабс = uотн + uпер
Добавим на рисунок величину ℓ и uэ, их нет в условии, но в природе они есть, и они связаны с законом сложения скоростей.
t0 – время спуска человека, скорость которого = 0
Свяжем величины, которые даны в условии задачи с величинами, которые есть на рисунке:
u1 + uэ = ℓ/t1 (скорость, которую видит наблюдатель за пультом эскалатора, когда смотрит на идущего по эскалатору)
u2 — uэ = ℓ/t2 (скорость, которую видит наблюдатель за пультом эскалатора, когда смотрит на вдвое быстрее идущего по эскалатору)
uэ = ℓ/t0 (скорость эскалатора или скорость стоящего человека, её видит наблюдатель за пультом эскалатора, когда смотрит на ступеньки или на неподвижного человека)
Перепишем первые два уравнения с учётом третьего и заменим u2 на nu1:
u1 + ℓ/t0 = ℓ/t1 — (1)
nu1 + ℓ/t0 = ℓ/t2 — (2)
умножим (1) на n:
nu1 + nℓ/t0 = nℓ/t1
вычтем (2) из последнего:
nℓ/t0 — ℓ/t0 = nℓ/t1 — ℓ/t2
разделим каждое слагаемое на ℓ:
n/t0 — 1/t0 = n/t1 — 1/t2
(n — 1)/t0 = (nt2 — t1)/t1t2
t0 = (n — 1)t1t2 / (nt2 — t1)
Анализ: при n = 1, получим t0 = 0? Т.е. стоящий на эскалаторе человек спуститься мгновенно?
Нет, при n = 1, окажется, что t2 = t1, а это значит, что получим дробь 0/0, но это мат.анализ 1 курс.
Колонна войск во время похода движется со скоростью 5 км/ч, растянувшись по дороге на расстояние 400 м. Командир, находящийся в хвосте колонны, посылает велосипедиста с поручением к головному отряду. Велосипедист отправляется и едет со скоростью 25 км/ч и, на ходу выполнив поручение, сразу же возвращается обратно с той же скоростью. Через какое время после получения поручения он вернулся обратно?
uк, ℓ, uв
t — ?
СО – земля:

Пока велосипедист едет, колонна продолжает движение, значит для передачи поручения он должен проехать расстояние больше чем ℓ, обратно наоборот.
СО – колона:

Относительно колонны, велосипедист туда и обратно проедет одинаковое расстояние l,(это будет использоваться в следующей задаче, поэтому важно понять) но если вспомнить поезда, идущие попутно и встречно (мы тогда сидели в электропоезде), то легко найти скорость велосипедиста относительно колонны для обоих случаев:
uк — uв – скорость велосипедиста относительно колонны при движении вместе с колонной,
uк + uв – скорость велосипедиста относительно колонны при движении против колонны.
Тогда, чтобы найти общее время, достаточно сложить время движения с одной скоростью, со временем движения с другой скоростью:
t=ℓ/(uв-uк) + ℓ/(uв+uк)=
(0,4 м·60 мин/20 км) + (0,4 м·60 мин/30 км) = 0,4·3 мин + 0,4·2 мин = 1,2 мин
Скорость катера относительно воды 7 м/с, скорость течения реки 3 м/с. Когда катер двигался против течения, с него сбросили в воду мяч. Затем катер прошёл против течения 4,2 км, повернул обратно и догнал мяч. Сколько времени двигался катер от момента сбрасывания мяча до встречи с ним?
uк, uт, Sпр
t — ?
СО – земля:

Предположим, что вода неподвижна, тогда если катер движется с uк, то нам не подойдёт Sпр, т.к. это расстояние пройдено против течения. Значит изучаем случай в СО – земля.
Свяжем величину, которая есть в условии задачи с величинами, которые участвуют в законе сложения скоростей, найдём tпр:
tпр = Sпр / (uк-uт)
СО – вода:
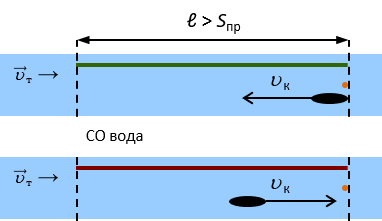
В СО связанной с водой или мячом, катер будет отплывать от мяча и приплывать к нему с одинаковой скоростью – uк, т.е. мяч никуда не переместился, значит:
tпр = tпо
t = tпр + tпо = 2tпо
tпр = 2Sпр / (uк-uт) = 8400м / 7 м/с — 3 м/с = 35 мин
Вывод. Можно менять СО решая одну и ту же задачу, в зависимости от того, какую ситуацию мы рассматриваем.
С угла A квадратного плота спрыгнул в воду и поплыл вокруг плота пес. Нарисуйте траекторию движения пса относительно берега, если он плывёт вдоль сторон плота, а его скорость относительно воды составляет 4/3 скорости течения реки.
uс = 4/3uп
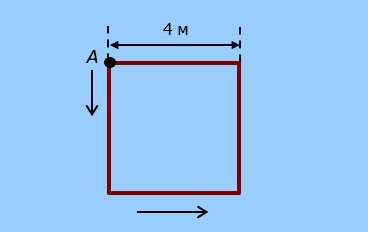
Если пёс, после прыжка, проплыл сторону плота, то сколько проплыл плот?
Если пёс и плот плывут одновременно, то у них время t одинаковое. Вычислим, на сколько переместился плот, если пёс проплыл его сторону перпендикулярно реке:
t = Sc/uc
t = Sп/uп
Sc/uc = Sп/uп
Sc·uп = Sп·uс
Sп = Sс·uп/uс = 4 м·3 м/с / 4 м/с = 3 м.
После того как пёс проплыл 4 м от т. А, плот проплыл 3 м:
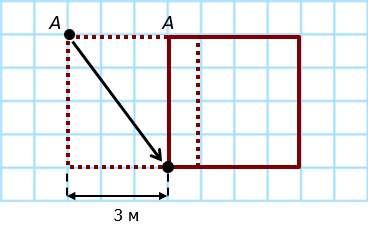
Далее, пёс плыл вдоль реки:
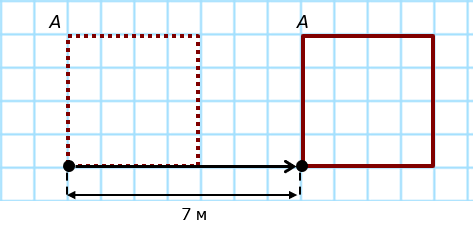
Затем снова перпендикулярно:
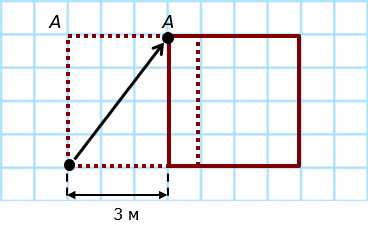
И наконец против течения:
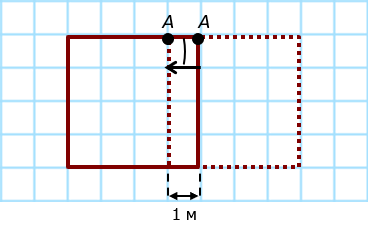
Траектория:

На лодке переплывают реку, отправляясь из пункта А (см. рисунок). Скорость лодки в стоячей воде u = 5 м/с, скорость течения реки u = 3 м/с, ширина реки S = 200 м. В какой точке пристанет лодка к противоположному берегу, если держать курс перпендикулярно берегам? Какой курс следует держать, чтобы попасть в точку В? Для обоих случаев определите время переправы.
u, u, S
ℓ, a, t1, t2 — ?
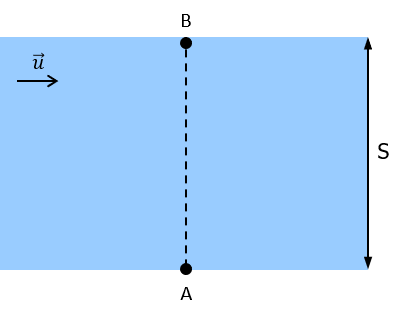
1-й вопрос – лодка держит курс ⊥ берегу.
Держать курс перпендикулярно берегам – это значит направить нос лодки перпендикулярно берегу, но т.к. есть течение – лодку будет сносить по течению
1-й способ. Рисуем вектор скорости лодки, нос которой направлен ⊥ берегам, затем перемещение лодки (АС) и снос относительно т. B (ℓ):
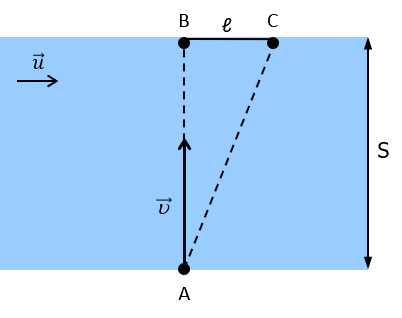
ℓ = tu
где t – время, в течение которого лодку сносило вдоль реки на расстояние ℓ, а также это время, в течение которого лодка плыла ширину реки S со скоростью u, тогда:
t = S/u
ℓ = S·u/u
t = 40 c, ℓ = 120 м
2-й способ, через закон сложения скоростей.
Если uотн – u и uпер – u, то uабс – u + u:
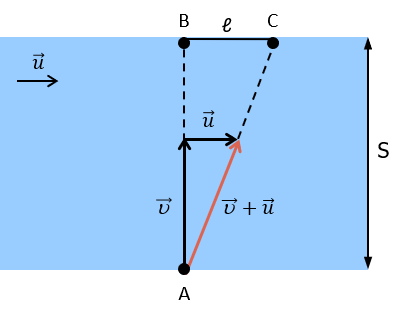
Треугольники перемещений(ABC) и скоростей подобны, значит:
u/u = ℓ/S
ℓ = S·u/u
Обратим внимание на то, что лодка одновременно участвует в двух движениях: вдоль вектора AB и вдоль вектора AC.
2-й вопрос. Лодка приплывает к т. В.
Чтобы попасть в т.В, нужно выяснить куда нужно направить вектор u, т.е. нос лодки. Для этого нужно учесть величину сноса течения, по которому нужно ориентироваться при повороте носа лодки. В этом случае, скорость лодки к т.B относительно берега – это uабс.
uабс = uотн + uпер или uабс = u + u
Нам даны вектор u и модуль u, остаётся их нарисовать так, чтобы их сумма получила вектор uабс
Найдём вектор u:
u = uабс – u, но сложением удобно, поэтому: u = uабс + (–u)
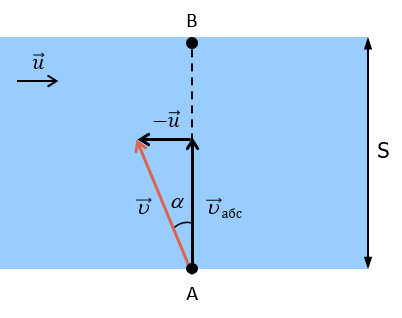
sin a = u/u
Под этим углом, нужно держать курс, чтобы попасть в т.B.
Теперь найдём время. Скорость, с которой лодка приближается к берегу – uабс = √u2 – u2
t = S/uабс = S/√u2 – u2
sin a = 0,6 => a ≈ 37°
t = 50c
Анализ: время переправы во 2-м случае больше, потому гипотенуза длиннее катета, ещё, скорость приближения к т.B (uабс) представляет лишь часть от скорости лодки u, потому другая часть представляет собой течение.
Капли дождя из-за сопротивления воздуха падают с постоянной скоростью u, перпендикулярной поверхности земли. Как необходимо расположить цилиндрическое ведро, находящееся на движущейся со скоростью u платформе, чтобы капли не попадали на его стенки?
u, u
a — ?
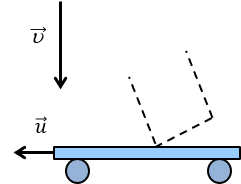
Нарисуем движение капли для наблюдателя на тележке:
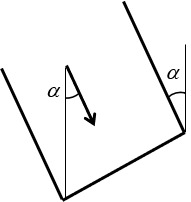
Капли не будут попадать на стенки ведра, когда они летят || стенкам ведра. А наблюдатель, сидя на тележке, видит их под углом a
Сопоставим наши скорости со скоростями закона сложения:
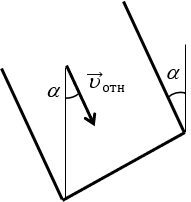
Если капли падают относительно земли, то u – это абсолютная скорость (uабс); если u – скорость движущейся СО, то это переносная скорость (uпер), тогда капли для сидящего на тележке падают с относительной скоростью(uотн).
Перепишем закон сложения скоростей:
u = uотн + u
Угол a будем находить зная uотн:
uотн = u — u
но сложением удобно, поэтому: uотн = u + (–u)
Нарисуем треугольник скоростей и угол a:
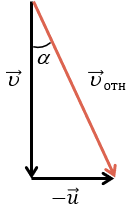
Под этим углом капли будут падать на дно ведра минуя стенки.
tg a = u/u
a = arctgu/u
Анализ: чем быстрее движется тележка, тем больше тангенс и тем больше угол.
0 Responses to “Относительность движения”